How Will MAP Measure the Basic Cosmological Parameters

How Will MAP Measure the Basic Cosmological Parameters?

Because MAP will be able to measure the microwave background fluctuations to tremendous accuracy with minimal systematic errors accross a wide range of angular scales, it should be able to accurately determine most of the basic parameters of cosmology. By answering many of the current open questions in cosmology, it will likely point astrophysicists towards newer and deeper questions. In order to understand how MAP will determine cosmological parameters, we will need to describe both the physical evolution of density fluctuations in the early universe and how cosmologists describe the statistical properties of the microwave background.

The History of the Universe

The big bang theory implies that the early universe was hot and dense. During the first three hundred thousand years of the big bang, the temperature of the universe exceeded 4000 K (7000 F), so most of the hydrogen in the universe was ionized. Thus, the early universe was a hot sea of protons and electrons. Since photons scatter off of the free electrons, the photons, electrons and protons are tightly tied together and behave as a single fluid. When the temperature of the universe dropped below 4000 K, the electrons and protons combined to make hydrogen. Hydrogen is almost completely transparent to the cosmic background radiation, thus, the photons can now propogate freely through the universe. The appearance of the sky on cloudy day is a good analogy to the appearance of the microwave background radiation. Water droplets scatter optical light, much like the free electrons scatter the cosmic background radiation. Water vapor is nearly transparent to optical light, just as neutral hydrogen is nearly transparent to the cosmic background radiation. On a cloudy day, we can look out through the atmosphere to the water droplets that make up the surface of the clouds. When COBE (and eventually MAP) observes microwave background sky it looks back to when there were free electrons that could readily scatter cosmic background radiation. This cosmic background "cloud surface" is called the "surface of last scatter" Thus, observations of the cosmic background radiation directly probe the physical conditions at this epoch, only three hundred thousand years after the big bang.

Evolution of Density Fluctuations

The

Microwave Background Fluctuation Spectrum

There are a number of effects that can produce temperature variations in the microwave background: variations in the density of the universe at the surface of last scatter, the velocity of the electron-photon fluid, variations in the gravitational potential of the universe at the surface of last scatter as well as variations in the gravitational potential along the photon path. As we will see different physical phenomenum are responsible for each of these effects so that by studying the microwave background fluctuations, we can infer a wealth of information about the early universe. Cosmologists find that it is convienent to represent the fluctuations in terms of an "angular fluctuation spectrum", which plots the amplitude of temperature fluctuation as a function of angular wave number l. Such a plot is shown below for the standard cold dark matter model in a flat universe.

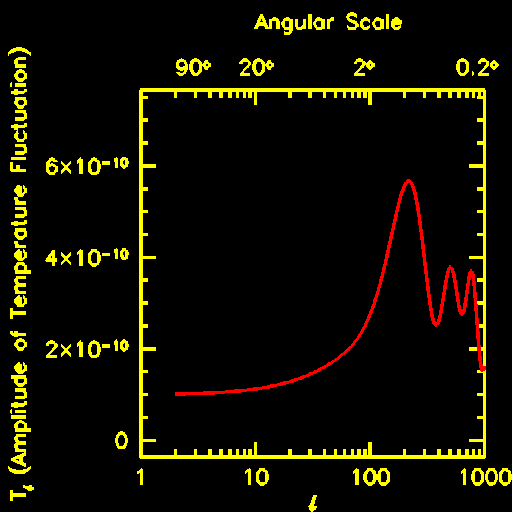
The temperature fluctuations are expected to be largest on the angular scale of roughly one degree. This scale corresponds to the angle subtended by the "sonic horizon", the distance that a sound wave moves from the beginning of the big bang to when hydrogen recombination occurs. This distance serves as a ruler for measuring the geometry of the universe.

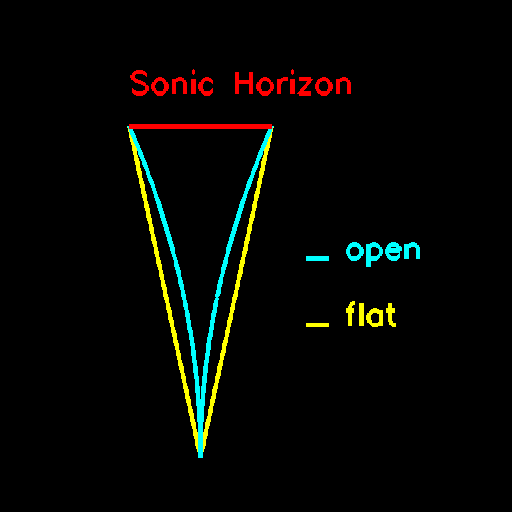
Measuring the Geometry of the Universe

In a flat universe, the dominant angular scale for microwave background fluctuations, the angle subtended by the sonic horizon at the surface of last scatter is roughly 1 degree. In our temperature fluctuation spectrum, this corresponds to l = 180. If the universe is open, photons move on more rapidly diverging paths in negatively curved space. Due to this effect, the dominant angular scale for microwave shifts to smaller angular scales (and hence larger l).

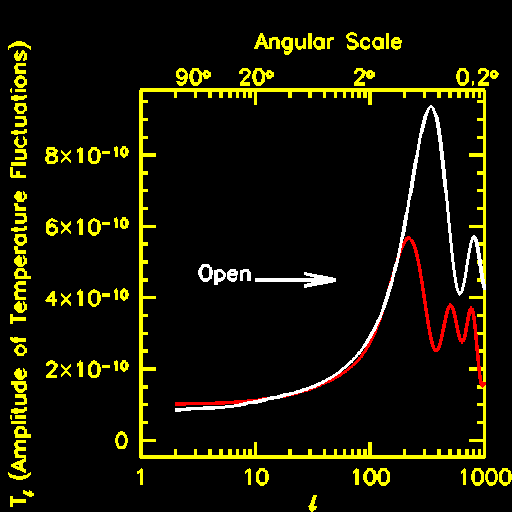
Counting the Number of Electrons in the Universe

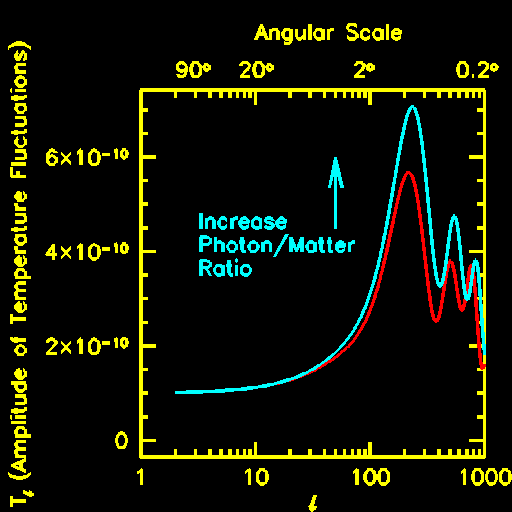
The behaviour of the early universe fluid will also depend upon the relative number densities of electrons and photons. The more electrons (and protons), the stronger their response to the gravitational potential wells. This leads to an enhancement of the first and third acoustic peaks, which are produced by the fluid falling into the potential wells and a suppresion of the second acoustic peak, which is produced by the fluid moving outward. Thus, by measuring the relative heights of the peaks in the fluctuation spectrum, we should be able to determine the relative number density of protons and electrons.

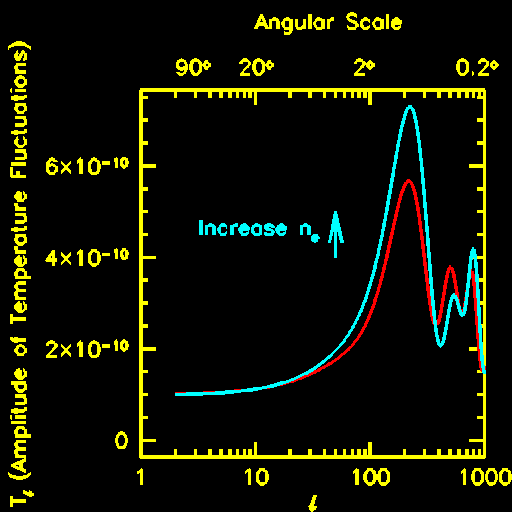
Increasing the ratio of electrons to photons also has the effect of decreasing the sound speed of the fluid. Since the fluid moves more slowly, the secondary oscillations occur at larger angular scales. This effect shifts the location of the latter peaks in the fluctuation spectrum.

Measuring the Matter Content of the Universe

The cosmic background radiation propogating from the surface of last scatter to our experiment is also affected by gravitational fluctuations along its path. Photons falling into the gravitational potential wells of clusters gain energy. They lose this energy when they climb out of the potential wells. If the universe is flat and composed entirely of matter, then these two effects cancel exactly and the matter along the photon path has no net gravitational effect. If there is a cosmological constant, then the depth of gravitational potential wells decay with time. Thus, a photon which falls into a deep potential well gets to climb out of a slightly shallower well. The net effect leads to a slight increase in photon energy along this path. Another photon which travels through a low density region (which produces a potential "hill") will lose energy as it gets to descend down a shallower hill than it climbed up. Because of this effect, a model with a cosmological constant will have additional fluctuations on large angular scales. Large angular scale measurements are most senstive to variations in the gravitational potential at low redshift.

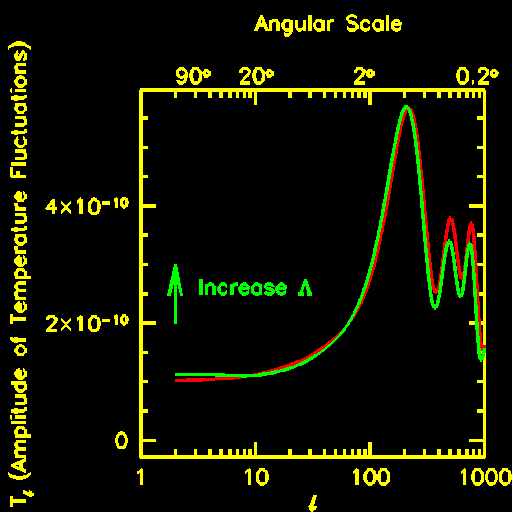
There is a similar effect operating at high redshift (z ~ 500 - 1300): during this epoch, photons and neutrinos make a significant contribution to the total energy density of the universe. Because of this contribution, gravitational potential fluctuations also decay during period. This leads to enhanced fluctuations on angular scales smaller than approximately two degrees. This is the angular scale subtended by the horizon at z ~ 500. The larger the ratio of photon energy density to matter density, the more important role radiation plays during this epoch and the higher amplitude of temperature fluctuations. Since the FIRAS measurements of the spectrum have already determined the photon energy density, we can use the measurement of the amplitude of fluctuations on this angular scale to determine the matter energy density.

Microwave Background Polarization: Another Window into the Early Universe

MAP measures not only temperature fluctuations in the microwave background, but also the polarization of the microwave background. While no one has yet detected microwave background polarization, our theoretical models predict that it should exist at an amplitude detectable with MAP's sensitivities. Scattered light, whether it is sunlight reflected off of haze, or microwave background photons that are reflected off of free electrons in the early universe is often polarized. This effect occurs because the electron-photon scattering cross-section depends upon the polarization of the incoming photon (which corresponds to the direction of the photon electric field). Because of this effect, we can probe the properties of the electrons that the photon encounters as it propogates from the surface of last scatter to our experiment. At this point in the discussion, the astute reader might object, "but wait, I thought that there were no free electrons left once the universe cooled below 4000 K". Fortunately, this is not true. Once stars start forming their radiation will be able to ionize hydrogen, thus liberating free electrons. These free electrons will produce polarization fluctuations in the microwave background that are potentially detectable.